Description
给定\(n\)个区间\([lo_i, hi_i]\),求最少移除区间数,使得剩余区间互不重叠
Constraints
要求时间复杂度不超过\(O(nlogn)\)
Solution
很多年前做过的题,就是反过来求的最多不重叠区间,结论就是按右端点排序。但是为什么呢?
如果不介意看我用Microsoft Paint 11.2205.9.0画出来的玩意,那应该可以解释一下
首先假设从左到右处理,最左端的若干区间并没有重叠部分,那我们自然是选择最左边的区间开始;但是如果有重叠部分呢?比如我们现在选取了最左边的左端点\(L_i\)对应的区间,现在存在重叠了,就有两种情况:可能是\(R_i > R_j\),也可能是\(Ri < R_k\)(注意\(L_i\)肯定是最小的),见下图
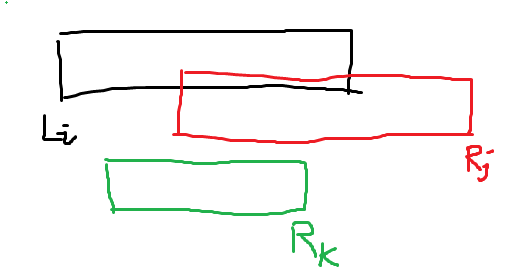
如果此时只能重新选择三选一,显然选择\(R_k\)对应的区间最划算。那能不能实现三选多?

如果是选择了\(R_k\),那确实有可能做到三选多,因为\(R_j\)在是上图有可能选中的(\(L_j\)的未确定性)
选完单个区间(右端点\(R_k\)对应的区间),子问题变成在剩下的未重叠空间内再次挑选
整个过程是很直观的,按右端点排序挑选,对\(R_k\)左边的空间来说都是合法可选的,对\(R_k\)右边来说是具有更大的挑选潜力
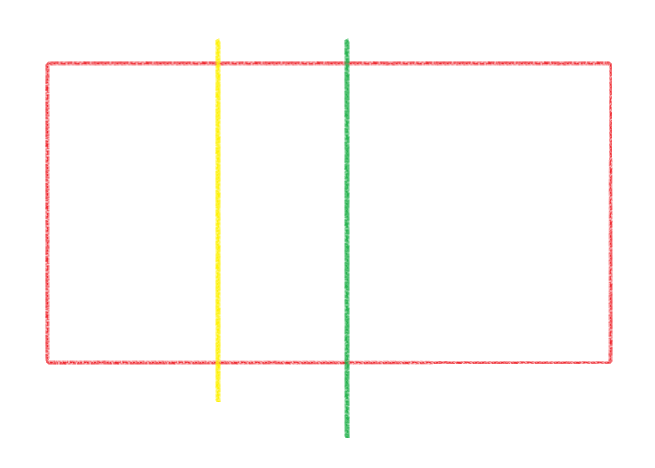
更抽象点来看,这个从左到右挑选的过程就像上图一样,整个框架对应若干区间的空间,黄色往右的区域得到的最优解肯定大于等于绿色往右得到的最优解
Code
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
auto &inv = intervals;
sort(inv.begin(), inv.end(), [](auto &l, auto &r) {
return l[1] < r[1];
});
int ans = 0;
int rmost = -1e5;
for(auto &i : inv) {
if(i[0] >= rmost) {
rmost = i[1];
continue;
}
ans++;
}
return ans;
}
};